기어가더라도 제대로
[알고리즘 스터디 with 케이시] 동적 계획법 본문
정의
- 해결한 작은 문제로 큰 문제를 해결하는 문제 풀이 방식
- 그리디나 백트래킹처럼 특정 알고리즘이 아닌 문제 해결 방식을 의미한다.
- Dynamic Programming(DP) 이라고도 부른다.
- 동적 계획법이 어렵게 느껴지는 원인 중 하나
- Dynamic 하지 않고 Programming 과도 관련이 없다.
- 메모리를 많이 사용하는 대신 빠른 성능을 자랑한다.
- 두 가지 방법론이 있다.
- 메모이제이션(Memoization)
- 타뷸레이션(Tabulation)
메모이제이션
- 하향식 접근법
- 동적 계획법에서 작은 문제들의 결과는 항상 같다.
- 따라서 이 결과들을 메모리에 저장해 필요할 때 꺼내 쓰는 것이 메모이제이션이다.
- 피보나치 수열이 주로 예시가 됨

- 위와 같이 있다고 할 때 중복되는 것들이 몇몇 있다.
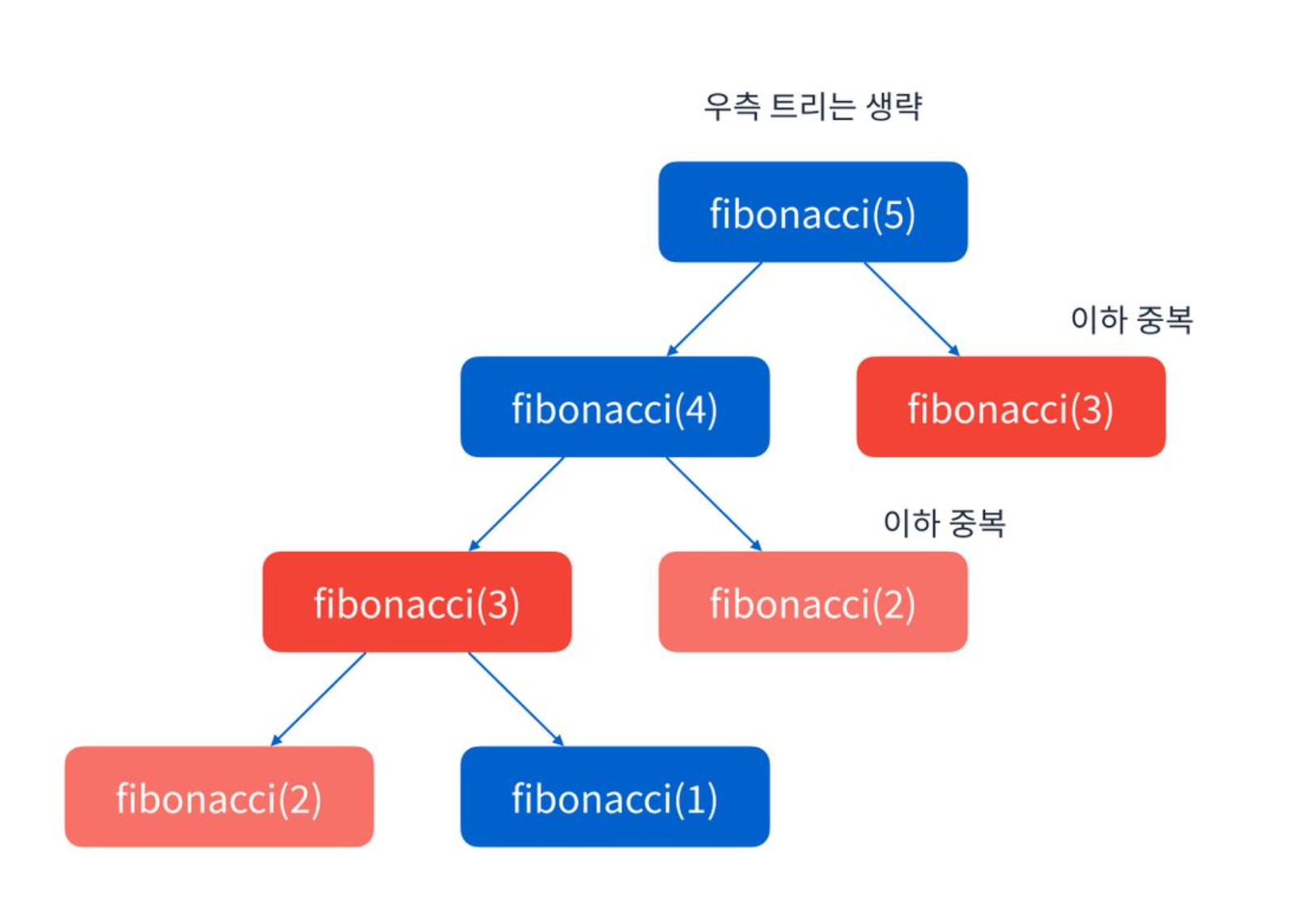
- 이미 해결한 문제는 기록해두면 성능 개선 == 메모이제이션
메모이제이션이 되기 위한 조건
- 이를 위해 가장 작은 문제를 기록해야한다.
fibonazzi(1)== 1 ,fibonazzi(2)== 1- 작은 문제로 큰 문제를 해결 할 수 있는가?

- 규칙이 있다면 가능하다.
- f(n) = f(n-1) + f(n-2)
타뷸레이션
- 상향식 접근법
- 필요한 값들을 미리 계산해두는 것
- 메모이제이션은 필요할 때 계산한다면(Lazy evaluation)
타뷸레이션은 미리 계산해둔다.(Eager evaluation) - 보통 코딩 테스트에선 메모이제이션을 쓰는 경우가 대부분이다.
- 꺼내쓸 때 상수 시간 밖에 걸리지 않는다.

동적 계획법 문제는 어떻게 접근할까?
- 동적 계획법 유형은 키워드만으로 동적 계획법 문제임을 알기 어렵다.
- 그렇기 때문에 문제 유형을 알 수 없다면, 다음을 확인해보자.
- 가장 작은 문제를 정의할 수 있는지?
- 작은 문제를 통해 큰 문제를 해결할 수 있는 규칙이 있는지?
- 위 두 가지가 가능하다면 동적 계획법 문제다.
- 간혹 메모리를 너무 사용하여 통과 못하는 경우도 있다.
- 이런 경우엔 백트래킹을 이용할 수 있지만 보통 코딩 테스트에서 자주 나오는 유형은 아니다.
출처
케이시
'CS > 자료구조' 카테고리의 다른 글
| [기초 자료구조] 약수의 합 구하기 (0) | 2022.10.21 |
|---|---|
| [알고리즘 스터디 with 케이시] 백트래킹 (0) | 2022.08.06 |
| [알고리즘 스터디 with 케이시] 투포인터 알고리즘 (0) | 2022.08.06 |
| [알고리즘 스터디 with 케이시]비트마스크 (0) | 2022.08.06 |
| [알고리즘 스터디 with 케이시] 최소 신장 트리 (0) | 2022.08.06 |
Comments



